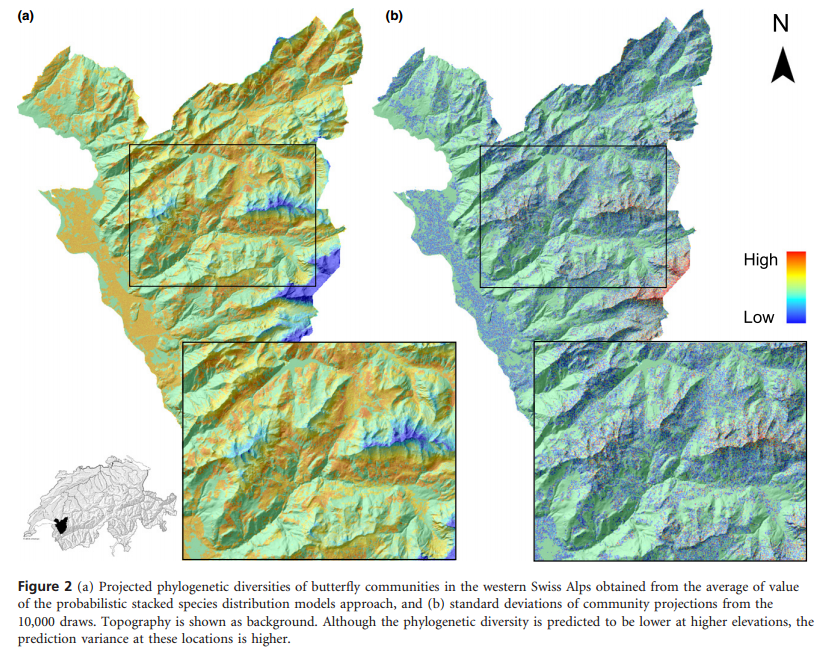
Pellissier, Loïc, et al. “A probabilistic approach to niche‐based community models for spatial forecasts of assemblage properties and their uncertainties.” Journal of Biogeography 40.10 (2013): 1939-1946.
Species distribution models (SDMs) are typically developed for a single species, because most of the time the goal is to predict habitat suitability for the occurrence of a single species. However, could there be more information about latent environmental traits, or about the probability of species occurrence in data on the presences of other species? Probably. These authors investigated an approach to predict uncertainty in predictions of community properties from stacked species distribution models. Stacked species distribution models are simply a set of independently trained species distribution models that are then laid on top of one another to predict community composition or species richness across a landscape. They don’t incorporate co-occurrence data directly, which is a flaw in my opinion, and this is recognized and has been tackled in other papers. To assess the ability of stacked SDMs to predict species richness, the authors compared a hard threshold approach (each binary SDM was converted into presence-absence predictions, the sum of the predicted presences formed the species richness in a given cell), and a probabilistic approach (each SDM predicted a probability, and these probabilities were compared relative to a 10,000 draws from a binomial distribution). The latter approach resulted in a stronger correlation between expected and observed species richness values. Further, the authors argue that this approach gets at uncertainty in model predictions, by using the variability from the 10,000 draws to get at uncertainty. This demonstrates the utility in considering community context in species distribution modeling. Methods directly incorporating information on co-occurring species will likely provide an even better view of the realized niche of species, or of community composition across a landscape.