A ecological niche can be defined (as by Hutchinson 1957) as the n-dimensional hypervolume that describes the environment allowing the species to exist. The hypervolume concept has been used to describe not only the niche of a species but also trait distributions of communities. Hypervolumes, as described by Blonder, can be convex describing the fundamental niche of a species where the boundaries of the area only have upper and lower limits. These can also be maximal where the boundaries are the available space representing the potential niche (the relationship between convex and maximal hypervolume concept relates to Drake 2015, Range Bagging). However, observed hyper volumes may have holes. These holes may be a result of not considered ecological or evolutionary processes of the species. Blonder developed an algorithm to detect holes within a hypervolume.
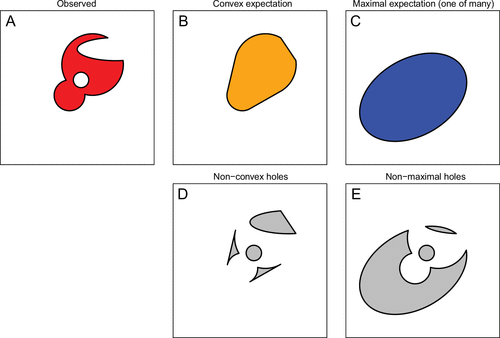
The Algorithm (an outline, featured image):
- Obtain input data in the form of an m x n matrix with m data points and n continuous, environmental variables.
- Compute a hypervolume H that encloses all data points using the hypervolume R function. The produces a stochastic geometry representation of the hypervolume, R_H
- Compute a hypervolume B with stochastic geometry representation R_B for the baseline expectation.
- Perform a stochastic geometry set difference S=R_B\R_H (all the points that are contained the baseline expectation (convex hull without holes) and the hypervolume with holes).
- Segment holes from the set difference.
- Remove small holes.
Using this algorithm with simulated data, Bolder found that Type I error rate (say there is a hole when there is not one) generally does not increase with data dimensionality. However, Type II error rate (say there is not a hole where there is one) does increase with dimensions, up to 100%. Also, increases in dimensions results in an exponential increase in runtime.

Blonder, B. 2016 Do Hypervolumes Have Holes? Am. Nat. 187, E93–E105. (doi:10.1086/685444)