Stoklosa, J. et al., 2015. A climate of uncertainty: accounting for error in climate variables for species distribution models R. B. O’Hara, ed. Methods in Ecology and Evolution, 6(4), pp.412–423.
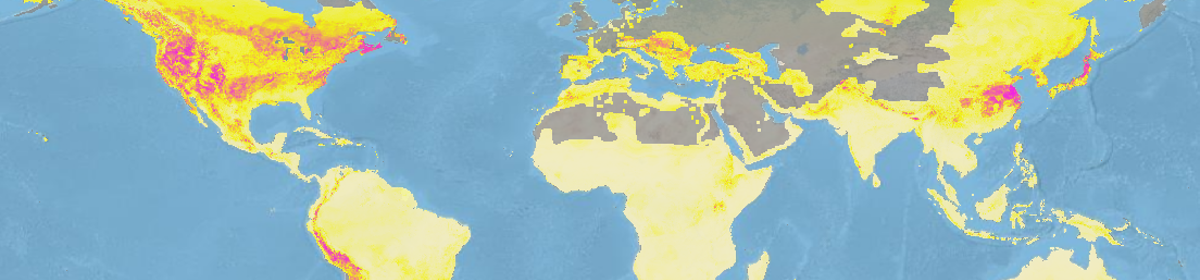
Climate variables used in species distribution models are estimates of true spatial climate and are therefore subject to uncertainty. The uncertainty itself can have spatial structure, further complicating consistency of estimates. The authors of this study chose to use PRISM (parameter elevation relationships on independent slopes models) to obtain estimates of climate uncertainty. To do this, they construct grids of approximately 800x800m size and use these estimates as an upper bound to prediction error variance of the climate model.
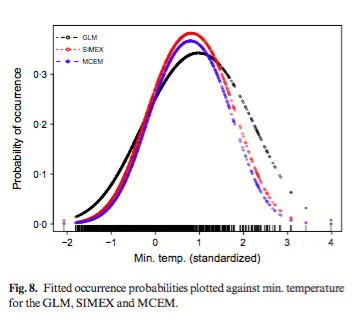
They also wanted to understand what happens if this uncertainty is ignored. Other fields, such as engineering and medicine, use measurement error models that allow uncertainty in explanatory variables (errors-in-variable) but can sometimes lead to biased estimates. This study used hierarchical modeling and simulation extrapolation to account for errors in explanatory variables. Wren presence/absence data (n=1048 data points) was obtained from birders at several points along a transect of the Eastern US. They test these methods on the Carolina wren in the US and on simulated species to look at how well GLMs predict and project to new scenarios when prediction error is ignored versus when it is accounted for. The main effect of ignoring uncertainty in climate variables was an increase in bias and a decrease in power as the error increases. These methods seem likely to be useful in situations where a species is patchily distributed or in environments that are spatially autocorrelated.