This study compared the likelihood functions used in species distribution modeling that have differences in occurrence records such as presence-only, presence-background, and presence-absence. Specifically, researchers focus on the differences of point and count data. Results indicate that the differences between the likelihood function of count data, and the likelihood function for point methods can originate from the same underlying inhomogeneous Poisson point processes model.
To first accomplish this, researchers provide an equation that allows for the consideration of continuous environmental space instead of discrete environmental space (equation 1). Researchers then adapt geographic space from discrete to continuous. They then provide considerations for the response type given either a discrete or continuous environmental/geographic space. After addressing these points, researchers then present the likelihood functions for unconditional inhomogenous Poissoin point processes and conditional inhomogenous Poisson point processes, and indicate how both functions are related to the Poisson log-likelihood.
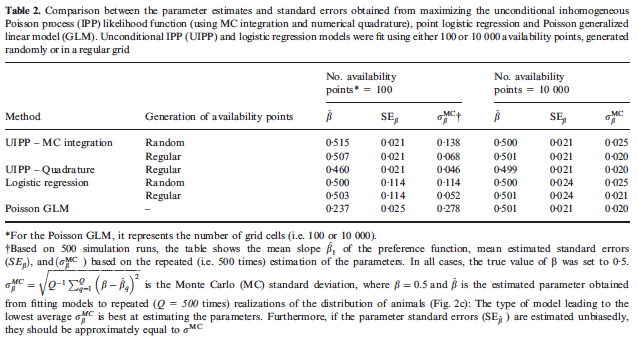
To asses how parameter estimates might vary across different realizations of the species range, researchers conducted a simulation and compared differences between IPP and logistic regression using either 100 or 10,000 availability points and one spatially autocorrelated environmental variable. To generate different parameter estimates the creation of environment and occurrence observation was repeated roughly 500 times. The mean estimates were compared to the true values; as well as, using Monte Carlo standard deviations. Most models were able to capture the true parameter value; however, the Poisson GLM performed poorly compared to all other models. The reason provided is because the scale the environmental covariate was distributed was much smaller than the resolution of the grid cells.