Naimi, Babak, et al. “Spatial autocorrelation in predictors reduces the impact of positional uncertainty in occurrence data on species distribution modelling.” Journal of Biogeography 38.8 (2011): 1497-1509.
This study investigates how using information regarding spatial autocorrelation of environmental variables can help mitigate the error introduced from positional uncertainty in species occurrence data. Spatial autocorrelation refers to the idea that for any given point in space of an environmental variable one would expect the nearby surrounding points to be more similar compared to those that are further away. Position uncertainty results from errors in determining where the geographical occurrence of the observation took place. In this study researchers used a simulated data set to observe how the interactions between spatially autocorrelated variables and positional error can influence the predictions made in both presence-only and presence-absence SDMs.
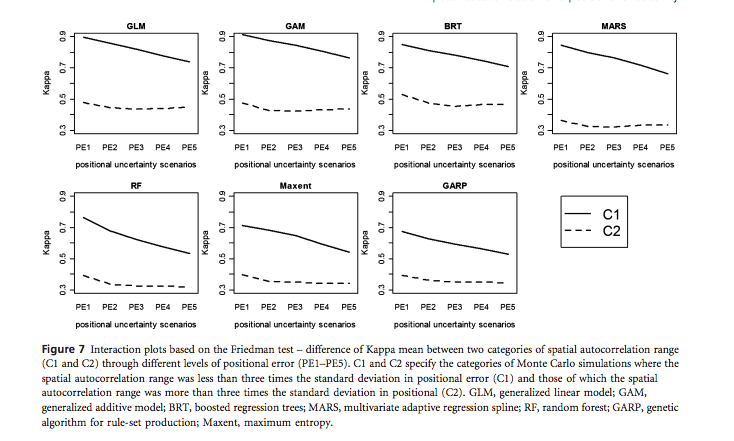
The simulated artificial data set was comprised of 2 environmental variables and one set of species observations that was linked to the environmental gradient. Researchers incorporated errors into their observation data based on a normal distribution, and then further propagated the uncertainty with Monte Carlo simulations. Species distribution models were evaluated using AUC and Cohen’s Kappa statistics. Cohen’s Kappa is a proportional measure that is variable to the set threshold detection level (unlike AUC). A two-way Friedman’s test was employed to asses if SAC in predictors reduced the influence of positional uncertainty.
Results showed that model performance varied depending on the trade between the degree of positional uncertainty and spatial autocorrelation in the provided data set. It is possible for spatial autocorrelation to reduce the impact of positional error; however, it is unable to fully compensate for error when positional error is extreme. Boosted regression trees, Generalized additive models, and Generalized linear models all outperformed random forests, Garp, and Maxent in terms of AUC. This is explained by the fact that the better performing models are presence-absence and thus have more information to make their predictions on.