The prevalence of a pathogen emerging in a population varies in a complex manner that is difficult to model and predict, due in part to randomness in the system. In a new paper in PLOS Computation Biology, we show that if the random component is relatively small, the underlying dynamics can be understood with the help of an analogy from physics, namely a damped harmonic oscillator, which can be depicted as an object sliding in a bowl filled with viscous liquid. When perturbed from its rest point, the object’s motion slows with the shallowness of the bowl. For small perturbations, we can approximate real pathogen dynamics with a similar system, but with the addition of noise (analogous to shaking the bowl).
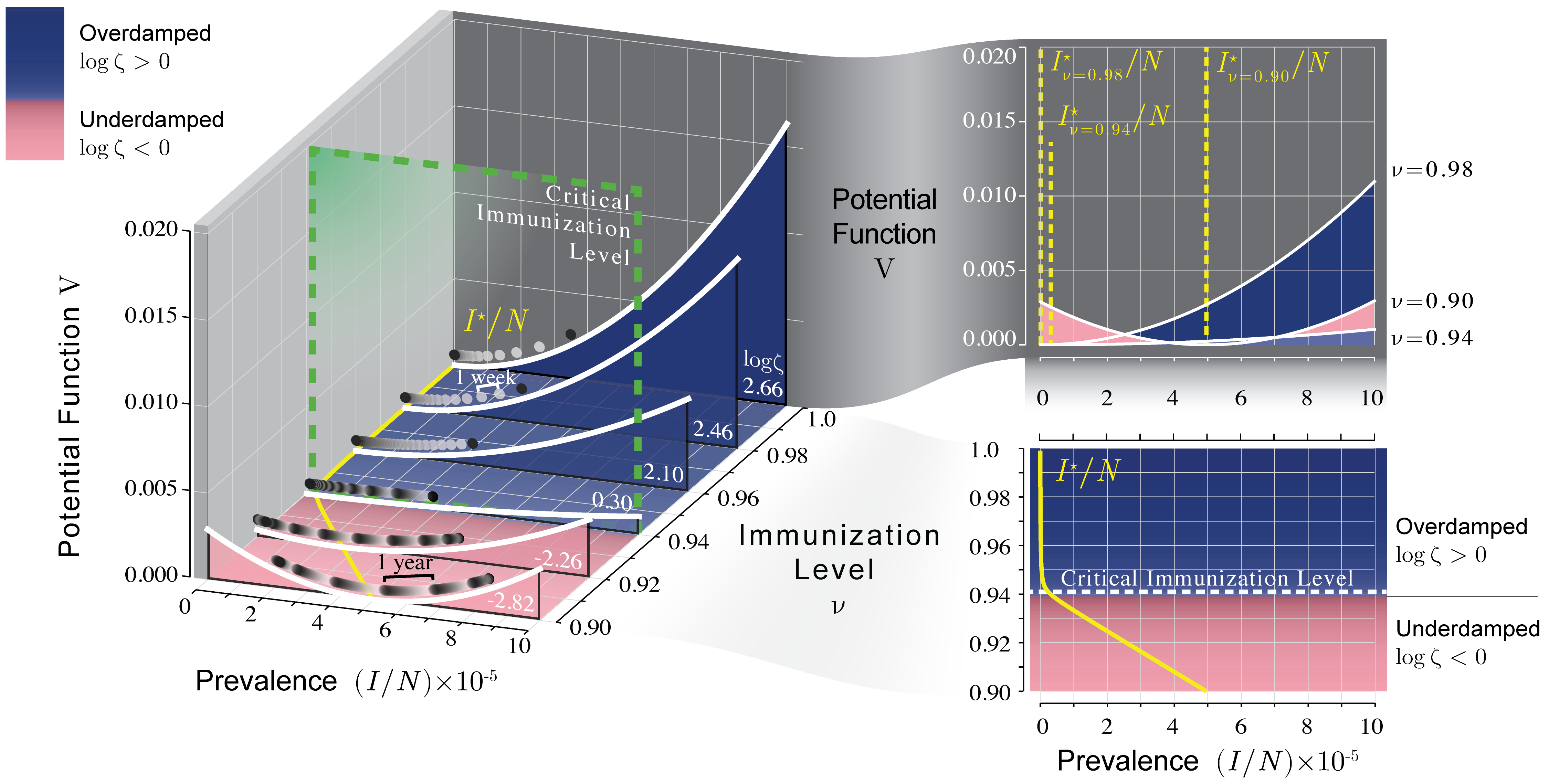
Illustration of critical slowing down in the potential function of the linearized SIR model. Disease prevalence (I/N) is represented by the horizontal position of a ball sliding through viscous fluid in a bowl with height determined by the potential function. Both the depth of the bowl and the viscosity of the fluid in the equivalent physical system are affected by vaccine coverage ν. The bowl is shallowest near the immunization threshold, which illustrates the slowing down of the dynamics as the critical point (ν ≈ 0.941, green dashed line) is approached. Oscillatory dynamics occur above immunization level ν ≈ 0.939, corresponding to the system becoming underdamped (pink region). Original figure online at https://doi.org/10.1371/journal.pcbi.1006917.g002
New statistical approaches to studying noisy systems can yield insight into these dynamics. We consider pathogen emergence as a critical transition from low prevalence to an endemic state. A critical transition occurs when small changes to system parameters (like vaccination rate) or small random fluctuations trigger positive feedback and rapid transition. As this critical transition is approached, the system exhibits a characteristic slowing down (as in shallower bowls), taking longer and longer to return to rest from each perturbation. This also happens when an endemic pathogen approaches elimination. Such critical slowing down, then, can be used to develop early warning signals for predicting approaching epidemics or imminent elimination. In the paper, we demonstrate how two such statistical early warning signals–variance and the autocorrelation function–have potential for anticipating disease emergence or elimination.
The paper is now available online:
Drake, J.M., T.S. Brett, S. Chen, B.I. Epureanu, M.J. Ferrari, É. Marty, P.B. Miller, E.B. O’Dea, S.M. O’Regan, A.W. Park, P. Rohani. 2019. “The statistics of epidemic transitions.” PLOS Computational Biology. https://doi.org/10.1371/journal.pcbi.1006917