Václavík, T. and R. K. Meentemeyer (2009). “Invasive species distribution modeling (iSDM): Are absence data and dispersal constraints needed to predict actual distributions?” Ecological Modelling 220(23): 3248-3258.
http://www.sciencedirect.com/science/article/pii/S0304380009005742
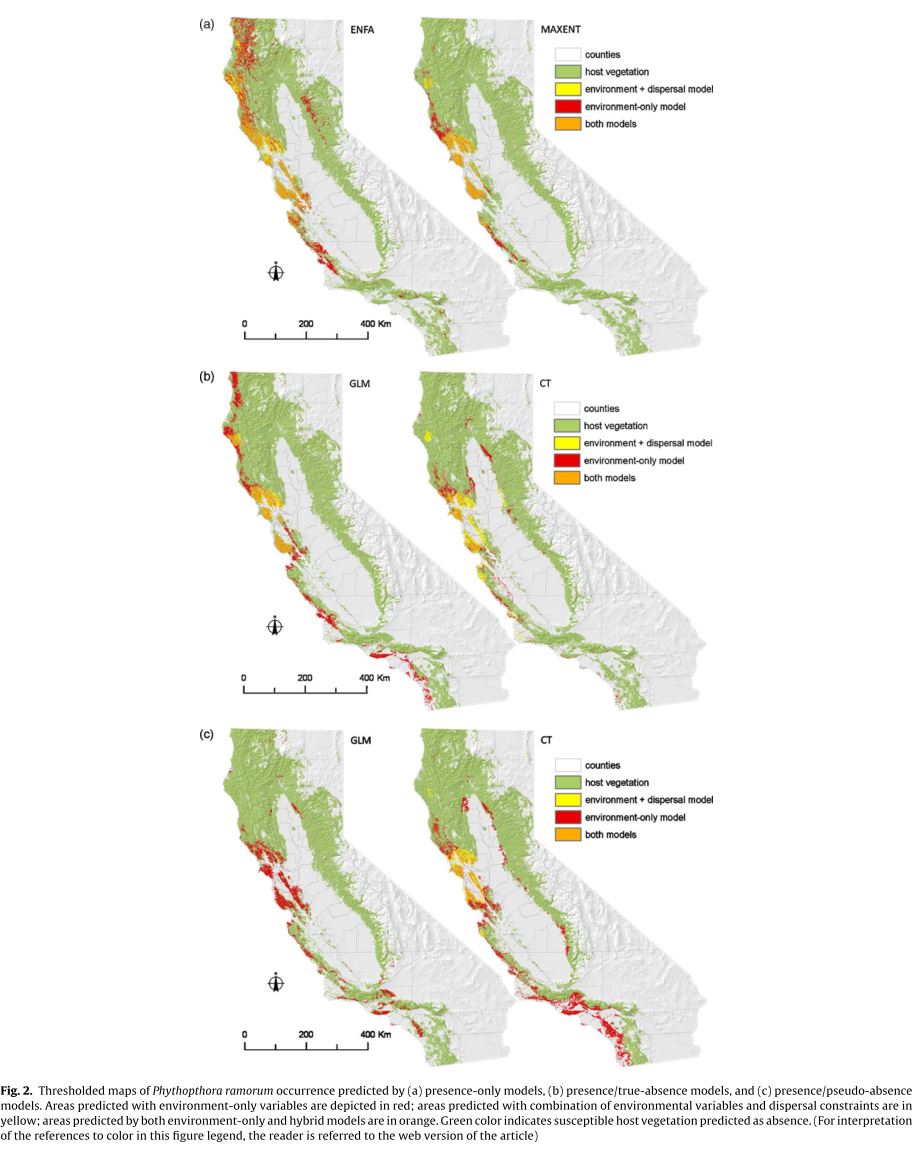
Vaclavik and Meentemeyeer focus on the specific problem of modeling the distribution of an invasive species in the process of invading across a landscape. iSDM forces the modeler to address the likely generally common problem of dispersal limitations because there will necessarily be a number of locations across the landscape which are environmentally suitable but currently inaccessible to the species. This paper examines how the addition of a measure of dispersal to iSDMs will affect the performance of models, alongside an attempt to determine the differences in performance of models trained using presence-absence, presence-psuedoabsence, and presence-only data respectively. The authors perform this analysis using Phytophthora ramorum an invasive generalist pathogen responsible for sudden oak death. 890 field plots were exhaustively sampled for evidence of the pathogen in the summers of 2003, 2004, and 2005, providing a reliable presence-absence data set. A number of pseudoabsences, points randomly chosen that could potentially be inhabited by the pathogen but which were not sampled, equal to the number of verified absences was also generated. Eight environmental variables were used to fit models including a spatial distribution of the key infectious host of the pathogen. All models were trained either exclusively on these environmental variables or on these variables and a measurement of “force of invasion” at a given point. Force of invasion was modeled using the following equation:
where djk is the Euclidean distance between each potential source of invasion k and the target plot i. The parameter a determines the shape of the dispersal kernel where low values of a indicate high dispersal limitation, and can only be estimated from presence-absence data. For models trained without true absence data a simpler force of infection metric based exclusively on the above-mentioned Euclidean distances is used. Two models using just presence-only data (ENFA, and MaxEnt) and two using presence-absence or presence-pseudoabsence (GLM and CT) were used. GLM and CT based on presence-absence data, including dispersal constraints were the highest performing models. The inclusion of dispersal constraints significantly increased the performance of most models. Without dispersal constraints presence-only models outperformed the other types of models (though this phenomenon was clearly driven by the good performance of MaxEnt). Presence-only models generally predicted larger areas of invasion than both presence-absence and presence-pseudoabsence but all models showed a clear reduction in predicted area when dispersal constraints were included. This paper clearly illustrates the importance of including probability of dispersal into SDMs for species in the process of invading a landscape. The estimates of “force of dispersal” seem as if they would suffer substantially from any sort of bias in the sampling of presence points but they may have been able to account for this in their sampling strategy. It would be interesting and useful to determine how these concepts could be applied to non-invasive species which nonetheless have dispersal restrictions preventing them from accessing some favorable areas of a landscape, allowing us to generally relax the assumption of equilibrium of distribution across the landscape. Such applications would likely require a more complex estimation of force of dispersal. In these closer to equilibrium cases there are likely landscape features which significantly slow the rate of dispersal across certain areas, which in turn creates the pattern, so we cannot assume an even rate of dispersal over time and space.