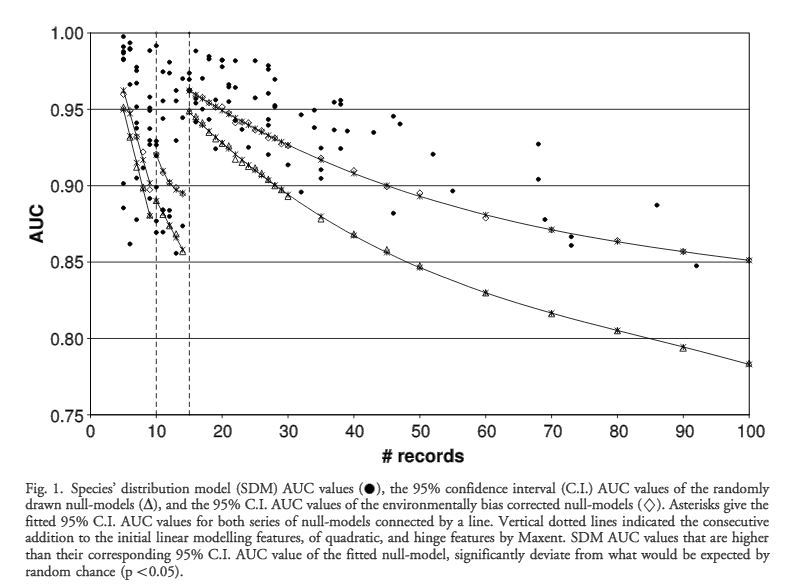
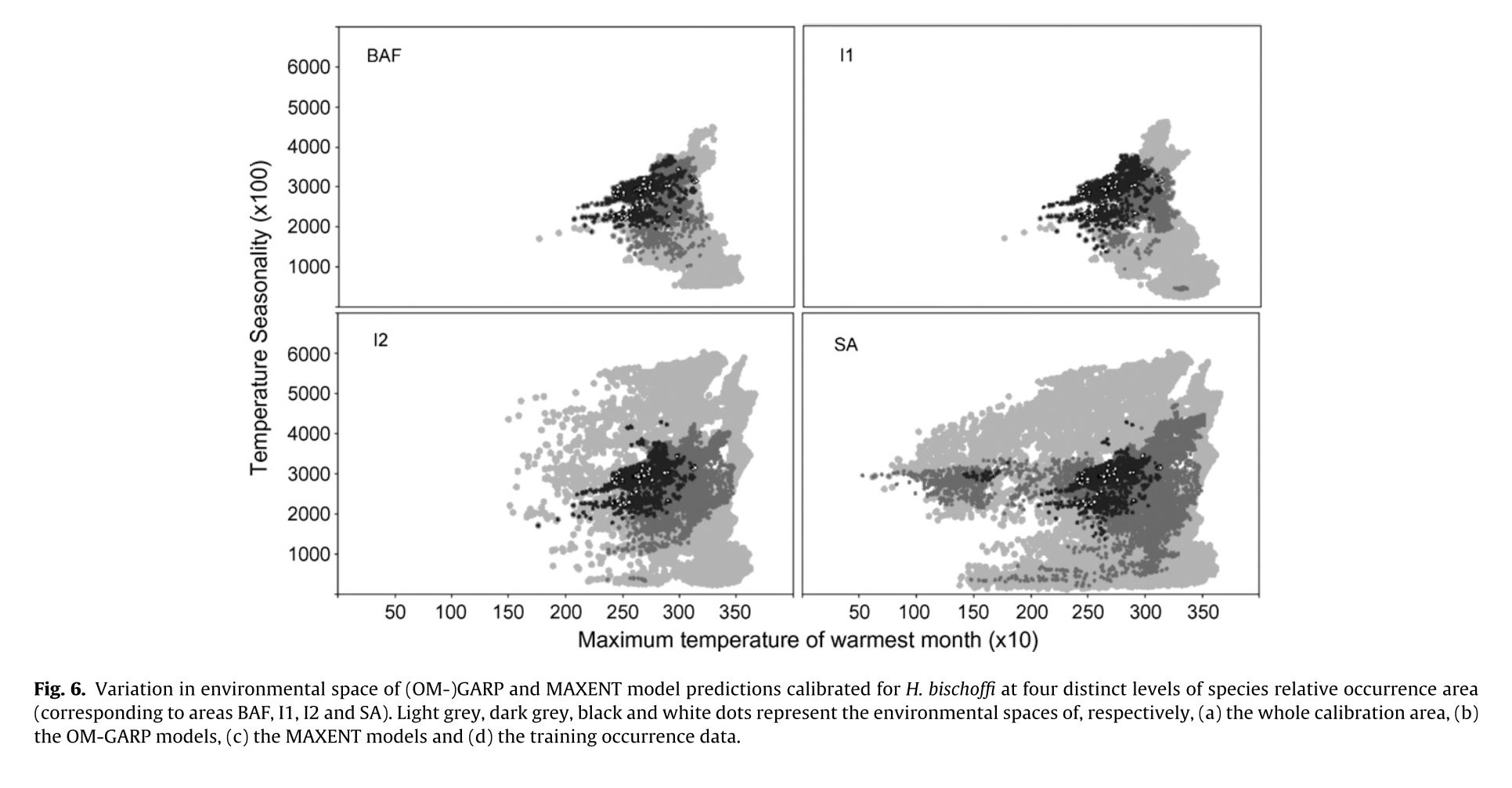
The authors set out to test the performance of five presence-only and presence-background SDM methods on sparsely recorded species in the neotropics. They use presence data on the common anuran Hypsiboas bischoffi to test the building of SDMs for species in the Brazilian Atlantic Forest (BAF). The models that they compare include: BIOCLIM (envelope based method in environmental space), DOMAIN (distance based method in environmental space), SVM (non-probabilistic statistical pattern recognition algorithms for estimating the boundary of a set), OM-GARP (a genetic algorithm which selects a set of rules that best predicts the distribution), and MAXENT. In addition to simply comparing the performance of these models in this region they also compare two alternative “calibration” domains for their models, the BAF and all of South America. “Calibration” domains defined the region from which pseudoabsence points were chosen for evaluation as well for training of presence-background models (OM-GARP and MAXENT). For those models that use pseudoabsence (OM-GARP and MAXENT) they examine how increasing calibration area (background) changes predictions in environmental space. These questions are relevant particularly in the Neotropics and more broadly because of the importance of modeling relatively unknown species with distributions of unidentified extents. Evaluation was performed using 5 random 75% training -25% testing partitions with 10 random pseudoabsences per occurrence point and assessed via AUC. Mean AUCs of models ranged from .77 (BIOCLIM/BAF) to .99 (MAXENT/SA). AUCs were always higher for models calibrated in SA than those in BAF. SVM had the highest AUC for BAF (.95) while MAXENT had the highest for SA (.99). BIOCLIM had the lowest AUC for both domains. The highest difference in predicted area for BAF vs. SA was OM-GARP’s. MAXENT was substantially more robust in its environmental predictions than OM-GARP to changes in extent of background area. As a result both SVM and MAXENT seem to be good choices for SDMs regardless of the unknown extent of the true distribution while OM-GARP may be a good option when the “calibration” area concurs relatively well with the extent of the “true” distribution. The most interesting results of this paper are the differences between OM-GARP and MAXENT in the way that their predictions are affected by a change in the extent of background points. This serves as yet another strong argument for MAXENT as a great choice model. Most of the remainder of the results seem to distill to the fact that evaluating in an increased area ought to lead to higher AUC because there are more obvious absence areas that are easily identified.

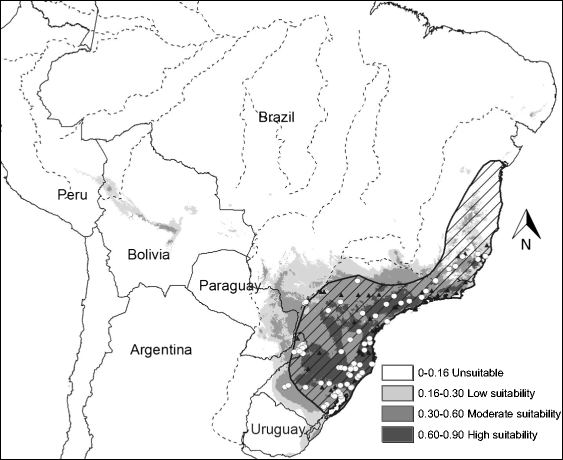
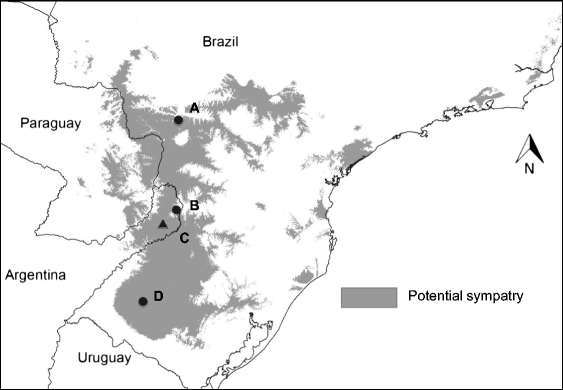
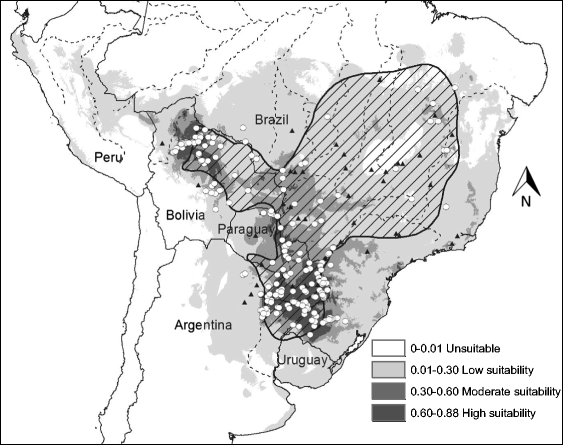 Habitat suitability (low, moderate, high) categorized the resulted of the predicted areas. In addition, the models were evaluated using AUC. Both the models provided a wider distribution than currently estimated. The results of the model for Alouatta caraya had a broader range and a variety of temperatures with Temperature Annual Range as the most influential to the distribution.
Habitat suitability (low, moderate, high) categorized the resulted of the predicted areas. In addition, the models were evaluated using AUC. Both the models provided a wider distribution than currently estimated. The results of the model for Alouatta caraya had a broader range and a variety of temperatures with Temperature Annual Range as the most influential to the distribution.