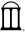Background  Few experimental or observational datasets are available from which to learn about the stochastic properties of extinction. Particularly, there have been no large studies from which the tail probabilities of extinction time could be estimated. This is key because (1) the idea that mean extinction time is useful for many applications has been almost universally rejected, and (2) data from many different kinds of complex systems have recently indicated that under some conditions many quantities of interest are governed by “fat-tailed” or “power-law” distributions, in which rare events are far more likely that implied by a distribution with exponentially small tails. This is important, because first passage times of supercritical Markov chains are well known to tend asymptotically to exponentiality and Markov chains are almost universally used to model the process of stochastic extinction. To determine empirically that the tail probabilities of extinction times are not exponential would present a major theoretical anomaly, as suggested by Keitt and Stanley (1998) concerning patch occupancy of North American breeding birds and weakly supported by Drake (2006).

Experimental Design   We conducted an experiment with >1000 populations of Daphnia pulicaria.  reared on the blue green alga Spirulina. Time-to-extinction in this experiment ranged over four orders of magnitude from 1 day to 1,239 days. The experiment is now complete with results only awaiting final statistical analysis.

Related Publications:

• Drake, J.M. 2014. Tail probabilities of extinction time in a large number of experimental populations. Ecology. (In press). http://dx.doi.org/10.1890/13-1107.1
• Drake, J.M. 2006. Extinction times in experimental populations. Ecology 87:2215-2220. [pdf]